7 IRUDI LAUEN AZALERA
Edozein irudi lauaren azlera kalkulatzeko, azalera kalkulatzeko moduko iruditan deskonposa daiteke.
2013(e)ko ekainaren 3(a), astelehena
2013(e)ko maiatzaren 27(a), astelehena
2013(e)ko maiatzaren 23(a), osteguna
KOKAPEN ERLATIBOAK
KOKAPEN ERLATIBOAK
8.1 Puntu baten eta zirkunferentzia baten kokapen erlatiboak.
1. Barruko puntua.
2..Zirkunferentziako puntua.
3.Kanpoko puntua.

8.2 Zuzen baten eta zirkunferentzia beten kokapen erlatiboak
1.Ebakitzailea.
2.Ukitzailea.
3.Kanpokoa.
8.3Bi zirkunferentzia kokapen erlatiboa
1.Zentrokidea.
2.Barruko ukitzailea.
3.Ebakitzailea.
4.Barrukoa.
5.Kanpoko ukitzailea.
6.Kanpokoak.
8.1 Puntu baten eta zirkunferentzia baten kokapen erlatiboak.
1. Barruko puntua.
2..Zirkunferentziako puntua.
3.Kanpoko puntua.

8.2 Zuzen baten eta zirkunferentzia beten kokapen erlatiboak
1.Ebakitzailea.
2.Ukitzailea.
3.Kanpokoa.
8.3Bi zirkunferentzia kokapen erlatiboa
1.Zentrokidea.
2.Barruko ukitzailea.
3.Ebakitzailea.
4.Barrukoa.
5.Kanpoko ukitzailea.
6.Kanpokoak.
2013(e)ko maiatzaren 14(a), asteartea
ZIRKUFERENTZIAK
Zirkunferentzia kurba itxi eta lau bat da, eta punto guztiak zentro izeneko 0 puntutik distantzia berera daude.
7.1 ZIRKUNFERENTZIAREN ELEMENTUAK
-Zirkunferentziaren zentroa: zirkunferentziaren puntu guztiak zentrotik distantzia berera daude.
-Erradioa: zentroa eta zirkunferentziaren edozein puntu elkartzen dituen zuzenkia.
-Korda: zirkunferentzia bi puntu lotzen dituen zuzenkia.
-Diametroa: zirkunferentziaren zentrotik igarotzen den korda.
-Arkua: zirkuferentziaren bi punturen arteko zatia da.
Korda bakoitzari bi arku dagozkio. Korda diametroa baldin bada, bi arkuen luzerak berdinak izango dira, eta arkuari zirkunferentzierdia deritzo.

Zirkunferentzia kurba itxi eta lau bat da, eta punto guztiak zentro izeneko 0 puntutik distantzia berera daude.
7.1 ZIRKUNFERENTZIAREN ELEMENTUAK
-Zirkunferentziaren zentroa: zirkunferentziaren puntu guztiak zentrotik distantzia berera daude.
-Erradioa: zentroa eta zirkunferentziaren edozein puntu elkartzen dituen zuzenkia.
-Korda: zirkunferentzia bi puntu lotzen dituen zuzenkia.
-Diametroa: zirkunferentziaren zentrotik igarotzen den korda.
-Arkua: zirkuferentziaren bi punturen arteko zatia da.
Korda bakoitzari bi arku dagozkio. Korda diametroa baldin bada, bi arkuen luzerak berdinak izango dira, eta arkuari zirkunferentzierdia deritzo.
2013(e)ko maiatzaren 13(a), astelehena
LAUKIAK
Laukiak lau aldeko poligonoak dira. Honela sailkatzen dira:
-PARALELOGRAMOAK: aldeak binaka paraleloak dituzten laukiak dira.
-TRAPEZIOAK: bi alde paralelo soilik dituzten laukiak dira.
-TRAPEZOIDEAK: alde paralelorik ez duten laukiak dira.
5.1 PARALELOGRAMOAK
Paralelogramoak honela sailkatzen dira.
 Karratua: lau ladeak berdinak ditu eta lau angelu zuzenak.
Karratua: lau ladeak berdinak ditu eta lau angelu zuzenak.
 Laukizuzena: lau angeluak zuzenak ditu.
Laukizuzena: lau angeluak zuzenak ditu.
 Erronboa: lau alde berdinak ditu.
Erronboa: lau alde berdinak ditu.
 Erronboidea: aldeak eta angeluak berdinak ditu, binaka, eta ez du angelu zuzenit
Erronboidea: aldeak eta angeluak berdinak ditu, binaka, eta ez du angelu zuzenit
5.2 TRAPEZIOAK
Trapezioak onelakoak izan daitezke:
 Trpezio angeluzuzena: Bi angelu zuzen ditu.
Trpezio angeluzuzena: Bi angelu zuzen ditu.
 Trapezio isoszelea: bi alde berdin ditu.
Trapezio isoszelea: bi alde berdin ditu.
 Trapezio eskalenoa: ez du alde berdinik ez eta angelu zuzenik ere.
Trapezio eskalenoa: ez du alde berdinik ez eta angelu zuzenik ere.
Laukiak lau aldeko poligonoak dira. Honela sailkatzen dira:
-PARALELOGRAMOAK: aldeak binaka paraleloak dituzten laukiak dira.
-TRAPEZIOAK: bi alde paralelo soilik dituzten laukiak dira.
-TRAPEZOIDEAK: alde paralelorik ez duten laukiak dira.
5.1 PARALELOGRAMOAK
Paralelogramoak honela sailkatzen dira.
5.2 TRAPEZIOAK
Trapezioak onelakoak izan daitezke:
PITAGORASEN TEOREMA
Triangelu angeluzuzenak angelu zuzen (90º) bat du. Angelu zzuzena osatzen duten aldeak katetoak dira , eta alde handiena, hipotenusa.
Triangelu honetan, b eta c katetoak dira, eta a, hipotenusa.
Triangelu angeluzuzenetan hau betetzen da: hipotenusaren berbidura katetoan berbiduraren baturaren berdina da.
PITAGORAS:
Pitagoras Samoskoa, grezieraz Πυθαγόρας, (Samos, k.a. 580 inguru – Metaponto, k.a. 495 inguru)Aintzinako Greziako matematikoari eta filosofo bat izan zen. Matematikoaren, Pitagorasen teorema gatik da ezaguna eta zenbakien bitartez dena azal daitekeela pentsatzen omen zuen.

Triangelu angeluzuzenak angelu zuzen (90º) bat du. Angelu zzuzena osatzen duten aldeak katetoak dira , eta alde handiena, hipotenusa.
Triangelu honetan, b eta c katetoak dira, eta a, hipotenusa.
Triangelu angeluzuzenetan hau betetzen da: hipotenusaren berbidura katetoan berbiduraren baturaren berdina da.
PITAGORAS:
Pitagoras Samoskoa, grezieraz Πυθαγόρας, (Samos, k.a. 580 inguru – Metaponto, k.a. 495 inguru)Aintzinako Greziako matematikoari eta filosofo bat izan zen. Matematikoaren, Pitagorasen teorema gatik da ezaguna eta zenbakien bitartez dena azal daitekeela pentsatzen omen zuen.
Harpidetu honetara:
Mezuak (Atom)
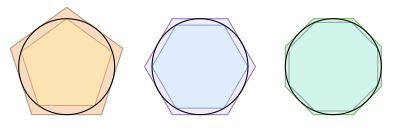
 A=perimetroa·apotema:2=P·a:2
A=perimetroa·apotema:2=P·a:2
 A=(B+B)·h:2
A=(B+B)·h:2
 A=oinarria·altuera:2 = b·h:2
A=oinarria·altuera:2 = b·h:2











